Using Fourier synthesis to generate a 3D landscape using simple trigonometry
Arguably the most impressive aspect of Lander is the lush green landscape into which most of us end up crashing again and again. It's this aspect above all others that creates such a realistic three-dimensional feeling to the game, and simply flying over the rolling hills and curved shorelines is such a smooth and serene experience that it really does show off what the ARM chip inside the Archimedes is capable of.

Perhaps even more amazing, though, is the method by which this landscape is generated. Let's take a look at how David Braben harnessed the power of maths to bring the green fields of Lander to life.
Procedural generation
---------------------
For students of Elite, it will come as no surprise to find that the landscape in Lander is procedurally generated; indeed, the origins of the algorithm described here can be found in the source code for the aborted sequel to 8-bit Elite (see the deep dive on Lander's origins on the ARM1 for details). Bell and Braben's classic BBC Micro game had no choice but to generate its 2000 star systems programmatically, as 32K is almost no memory at all, but it isn't such a clear-cut decision when it comes to Lander.
The first Archimedes machines boast memory specifications that made us Beeb owners drool back in the day; even the entry-level A305 comes with 512K of fully mapped RAM, a good four times the amount of memory in the BBC Master and 16 times that of the original BBC Micro. And these older machines had to rely on bank-switching to squeeze it all into the 6502's 8-bit memory map, while the Archimedes is the opposite, with a logical memory map that far outweighs the physical memory available (see the deep dive on the Lander memory map for more on this).
So given all this memory, why can't we just store all of the game's landscape coordinates in memory and be done with it? Well, we possibly could, if were OK with limiting the landscape to, say, a repeating square pattern of 256 x 256 tiles, with the screen showing a 12 x 10 tile portion at any one time (note that the game's object map is finite and repeats every 256 x 256 tiles, so this is a sensible size to choose for this hypothetical situation). The shape of the landscape is defined by the altitude of the landscape at each tile corner, so the whole tile-shape of the landscape can be stored in 256 x 256 altitude values, so that's 65,536 numbers. As it stands, Lander calculates landscape heights as 32-bit values, so that would take up 256K of RAM, though you could probably get this down to at least half of that by dropping down the accuracy and squeezing multiple values into single words.
But even 128K is too much memory for a game that absolutely has to work in the Archimedes A305 (this game was commissioned by Acorn to show off all of their machines in their new range, after all). In the event, Lander needs 172K of memory in which to run, and to fit this into an A305 you have to disable the desktop, font and window managers. Adding 128K for the landscape was never going to be an option.
On top of this, we need more accuracy than a 256 x 256 grid could give us. For example, we need sub-tile altitude figures when calculating the shadows that Lander drapes over the landscape beneath objects like the player's ship, trees and gazebos. We could probably make-do with a pre-calculated grid, but the result wouldn't be as smooth as the luscious shadow effects we see in Lander. And the shadow calculations are also used to detect certain types of collision with the ground, and accuracy is all-important when it comes to triggering crashes.
Luckily procedural generation is something that David Braben knows a thing or two about, so let's look at how the landscape in Lander actually works.
Fourier synthesis
-----------------
Instead of storing 65,536 landscape altitudes, Lander calculates each altitude on-the-fly. The GetLandscapeAltitude routine does the heavy lifting, taking a tile corner coordinate in the form (x, z) and returning the altitude of that corner.
Before we jump into the altitude generator itself, we need to talk about the coordinate system in Lander. Lander uses a right-hand coordinate system, with the x-axis pointing from left to right, the y-axis pointing down, and the z-axis pointing into the screen. It's called a "right-hand" system because if you take your right hand and point your thumb, index and middle fingers at right angles to each other, then each of your fingers will point in the same direction as each of the three axes. Elite uses a left-hand coordinate system because its y-axis points up, not down, but Lander flips the y-axis so it matches the y-axis on the computer screen, making things a bit easier to follow when swapping between 3D world coordinates and 2D screen coordinates.
As the landscape runs into the screen and away from us, points on the landscape can be described by an x-coordinate (for left to right) and a z-coordinate (for going into the screen). The altitude of a point on the landscape is therefore the y-coordinate of that point (for the up-down axis). If you imagine the landscape being a paper map, then the x- and z-coordinates are the longitude and latitude for points on the map, and the y-coordinate is the contour value shown on the map.
So, to the procedural generation. Take a deep breath, because the altitude of a point (x, z) on the landscape in Lander is calculated as follows:
LAND_MID_HEIGHT - ( 2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z)
) / 256
This looks like arcane magic, but once you understand what's going on, it's actually quite straightforward. This algorithm is based around an area of maths called Fourier analysis, which is the study of how we can break down complicated mathematical functions into a sum of simpler trigonometric functions; Fourier synthesis is the name for going the other way, from trigonometric functions to complicated functions, which is what Lander uses to generate the landscape. If you want to know more about this then the Wikipedia entry on Fourier analysis is not a bad place to start, but let's see if we can explain this less mathematically and more intuitively.
Imagine a completely placid swimming pool. If you make a splash in one corner, then a wave spreads out from that splash across the whole pool. Ignoring any reflections from the sides (let's just pretend they don't happen), the splash travels through the water, making a wave shape as it goes. Here's an example of a typical wave shape, set off by a splash in the bottom-right corner of the graph:
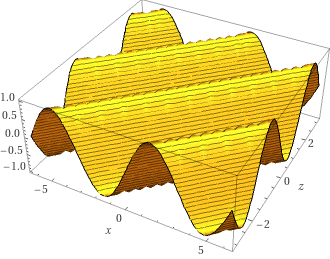
And here's another, this time sending a wave from left to right:
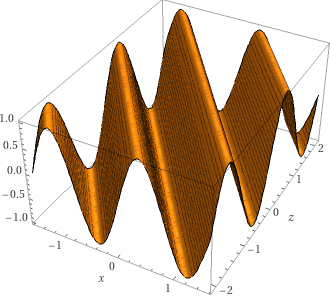
If we make these two splashes at the same time, then the waves combine to look like this:
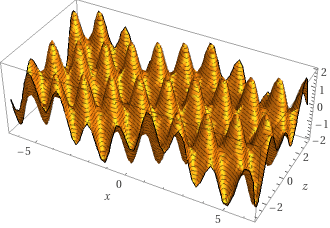
If you look at the result, you can see the effects of one wave travelling from left to right, and the other travelling into the screen.
Waves like this are mathematically very simple. Just like sound waves or radio waves, water waves are represented mathematically as sine waves. This is a sine wave:
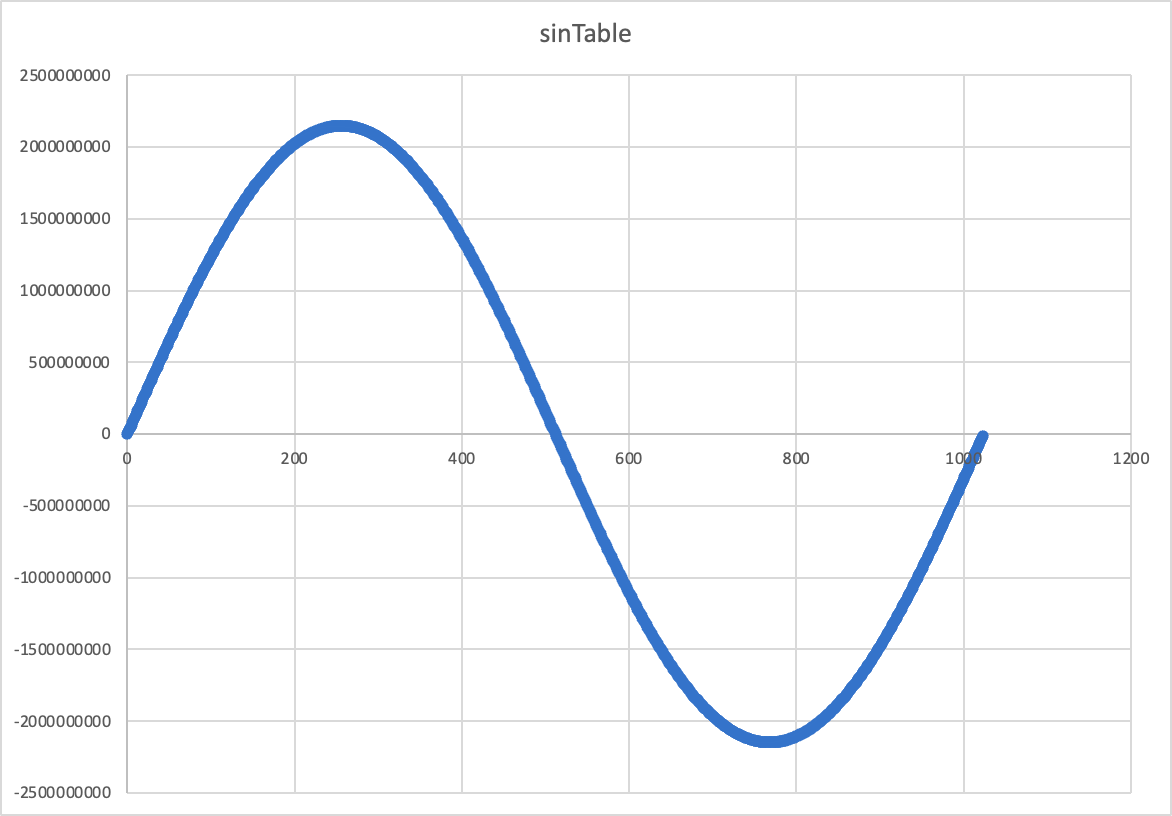
Indeed, this sine wave is the one that is stored in Lander, in the sinTable variable, which the game uses to calculate sine and cosines quickly, by simply looking up the relevant entry in the table.
Let's look at the above waves a bit more mathematically, then. The first graph above shows this formula:
y = sin(x - 2z)
while the second shows this:
y = sin(4x + 3z)
You can see these results in Wolfram Alpha, for the first formula and for the second formula (that's where I got the graphs from - it's a great resource).
To combine two sine waves mathematically, we can simply add them together. So the third graph shows this formula:
y = sin(x - 2z) + sin(4x + 3z)
which you can see in Wolfram Alpha here.
So, adding sines together combines the shapes of the individual sine waves. If you look at the procedural generation formula that Lander uses:
LAND_MID_HEIGHT - ( 2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z)
) / 256
then you can see that it is just a sum of six sines, with some of them multiplied by two. This figure is then divided by 256 and is subtracted from a constant, LAND_MID_HEIGHT, that represents the altitude of the vertical mid-point of the landscape... and that's it. (For more on the mid-point part of the calculation, see the next section below.)
So it might look like a complex formula, but it simply represents the merging of six different waves in our swimming pool, being set off in different directions and from different places around the pool edge. The ones that are multiplied by two are effectively splashing twice as hard as the others, but they are still sine waves, just deeper ones.
If we add all the waves in the landscape formula together, including the factor of 2 for the first four waves, and then negate the result, then we get this formula:
y = -( 2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z))
which looks like this when fed into Wolfram Alpha:
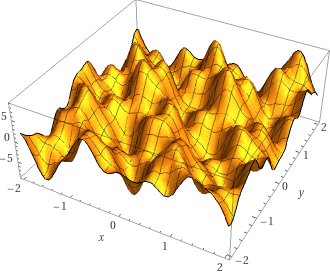
So this is the state of our swimming pool with all that splashing, and it's really starting to look like a landscape rather than a set of sine waves.
That's where the final aspect of the landscape generator comes in, and that's to create the sea. In the above sum-of-sines, the entire landscape is made up of valleys and peaks, but in Lander we flood the world by simply capping the altitude value that we return, so that it never goes below sea level. If we apply this to our graph, then we get this:
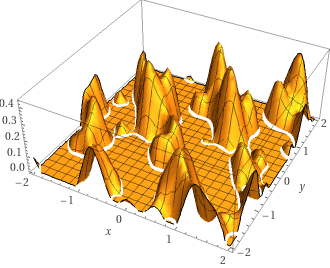
And this is the landscape in Lander, all generated by adding sine values, which are quick to generate using nothing more than a sine lookup table. We already need the sine lookup table for other parts of the code, so the only storage cost for this procedural approach is for the GetLandscapeAltitude routine, which contains just 46 instructions.
And for fans of Zarch, the more fully featured game that David Braben wrote next, using the Lander engine, it's interesting to compare a contour map of the above equation with the radar in Zarch. Here's the contour map from Wolfram Alpha:
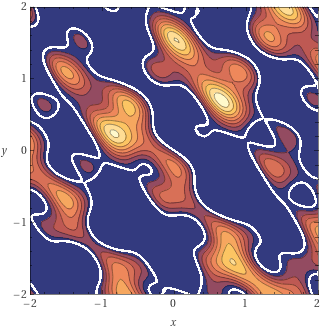
and here's a close-up of the Zarch radar:

Zarch clearly uses a different set of sine waves to generate its landscape, but you can see that it's the same process.
Finally, it's worth noting that although the landscape appears to be infinite, it actually repeats periodically, just like the trigonometric functions from which is composed. In the case of Lander's landscape, the non-repeating landscape covers the range:
0 <= x < 2 * PI 0 <= z < 2 * PI
because the sine lookup table at sinTable contains 1024 values of the form:
(2^31 - 1) * SIN(2 * PI * (n / 1024))
and this repeats every 1024 values of n. If we apply this range to our graph, then we get this:
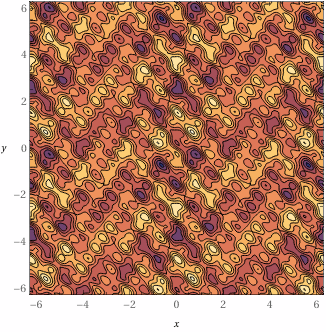
To make things more obvious, the range of this graph is double the period, so that's -2 * PI to 2 * PI in both axes. This means that the image shows four repeated squares of landscape, in the top-left, top-right, bottom-left and bottom-right. You can see that the repeated squares tessellate seamlessly, giving the impression of an infinite landscape when it's actually periodic.
And because the sine table divides n by 1024, the range in terms of landscape tile coordinates is this:
0 <= x < 1024 0 <= z < 1024
which is easily big enough to make the game feel infinite. It's all very impressive.
Scale and parallel waves
------------------------
The above swimming pool analogy is a bit of an over-simplification, and for completeness it's worth mentioning why.
First, making a splash will send out sine waves in a circle, all emanating from the splash point, but the sine waves in the above model are travelling along a straight line, much like a tsunami hitting an entire shoreline at once. So, strictly, we should either be generating our splashes from a very long way away rather than the side of the pool, or we should be generating them by slapping long logs into the water so they send out parallel waves. I thought I'd leave out this detail to keep things simple.
Second, as mentioned above, swimming pools have sides, and waves reflect off the sides, so if you did this experiment in a real pool, you would quickly get some really chaotic motion as each wave reflected back into the pool. To be accurate, I guess our pool should be in the middle of a placid lake, with us setting off waves from platforms above water level, but if you just ignore the side of the pool, that will do the same job.
Finally, let's look at the LAND_MID_HEIGHT part of the equation. Each square landscape tile in Lander is &01000000 wide in terms of 3D world coordinates, and the vertical mid-point of the landscape in LAND_MID_HEIGHT is defined as five tiles in size, so LAND_MID_HEIGHT has a value of &05000000. That means that our formula:
LAND_MID_HEIGHT - ( 2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z)
) / 256
is the same as this:
&05000000 - ( 2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z)
) / 256
The range of values returned by the sine function runs from -1 to +1, and this signed value is stored in the sine lookup table using the full 32 bits, so the range of sine value in the table runs from &80000000 (for -1) to &7FFFFFFF (for +1).
We add up four doubled sine values and two straight sine values in that part of the calculation, like this:
2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z)
So that's the same as adding up ten sine functions.
We also divide the result by 256, which we implement in the code by dividing each sine value by 256 before adding them up, so we don't overflow the addition. This means that after being divided by 256, each individual sine is in the range &FF800000 to &007FFFFF, and the range of the sum of ten of these is therefore:
- At the lower, most negative bound: 10 * &FF800000 = &FB000000
- At the higher, most positive bound: 10 * &007FFFFF = &04FFFFF6
This means that that the range of this part of the formula:
( 2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z)
) / 256
is &FB000000 to &04FFFFF6, so the range of the complete formula:
&05000000 - ( 2*sin(x - 2z) + 2*sin(4x + 3z) + 2*sin(3z - 5x)
+ 2*sin(3x + 3z) + sin(5x + 11z) + sin(10x + 7z)
) / 256
is &00000004 to &09FFFFF6, or an altitude of 0 to 10 tiles (with the mid-point in LAND_MID_HEIGHT at an altitude of 5 tiles). Sea level is defined in the SEA_LEVEL configuration variable as a value of &05500000, which is just below halfway (because the y-axis increases as it goes downwards).
So the generated landscape is between 0 and 10 tiles high, with the lower 47% of this landscape flooded to create the landscape that we know from the game.
I hope this gives you comfort when you're face-planting yet again into the sinusoidal slopes of David Braben's procedural landscape.